Exercice : Cas de l'Amibegron
Cette molécule a la structure suivante :
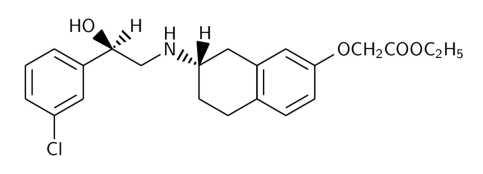
\({\rm M}_{\rm m}\) = 440,37 g/mol
Nous avons ici une entité chimique qui a été développée sous forme d'un sel, en l'occurrence un chlorhydrate.
Pour simplifier, nous supposerons que deux formes cristallines vraies, dénommées A et B, ont été identifiées dans le cadre du triage polymorphique. Les paramètres de mailles des deux formes sont donnés ci-dessous :
Forme A | Forme B | |
|---|---|---|
Formule chimique | \(\ce{C22H27N1O4Cl2}\) | \(\ce{C22H27N1O4Cl2}\) |
Poids moléculaire | 440,37 | 440,37 |
Système cristallin | orthorombique | orthorombique |
Groupe d'espace | P2,2,2 | P2,2,2 |
Paramètres de maille : \(a\ (Å)\) \(b\ (Å)\) \(c\ (Å)\) |
14,6119 14,7939 21,7429 |
6,5651 14,3500 22,8325 |
Z | 8 | 4 |
Volume (\(Å^3\)) | 4700 | 2151 |
Masse volumique (kg/m\(^3\)) | 1247 | 1360 |
Une analyse par ACD[2], menée à \(20\ °\textrm{C.min}^{-1}\), fait apparaître pour chaque forme un pic de fusion dont les caractéristiques sont les suivantes :
Forme A : | \(T_{f,\,A} = 158\textrm{ °C}\) | \(\Delta h_{f,\,A} = 65\textrm{ J.g}^{-1}\) |
|---|---|---|
Forme B : | \(T_{f,\,B} = 128\textrm{ °C}\) | \(\Delta h_{f,\,B} = 85\textrm{ J.g}^{-1}\) |
Question
Quelle est la relation thermodynamique reliant \(A\) et \(B\) ?
Donner l'allure du diagramme \(G\left(T\right)\) pour les deux formes.
Votre réponse se trouve-t-elle confortée par l'examen des masses volumiques théoriques telles que présentées dans les tableaux ?
On effectue alors pour les deux formes une détermination des cinétiques de dissolution intrinsèques, soit \(J^A\left( T \right)\) et \(J^B\left( T \right)\) dans un milieu aqueux de\(pH=3\), avec une rotation de 100 tours/min et à 37 °C. La figure ci-dessous récapitule les données observées en \(\textrm{mg/cm}^2\) de produit dissout en fonction du temps.
Question
D'après ce résultat, quelle est la forme la plus stable à 37 °C ?
Cela vous permet-il de préciser un peu plus le diagramme \(G\left( T \right)\) tracé précédemment ?
On effectue cette même détermination à plusieurs températures et on trace ensuite un diagramme type Van't Hoff \(\ln \left( J \right) = f\left( \frac{1}{T} \right)\) pour les deux formes. On obtient les courbes suivantes :
On obtient un point de croisement pour la forme \(A\) (bleu) et la forme \(B\) (rouge) situé à une température de 63 °C.
Question
Cela vous permet-il de compléter votre connaissance de la thermodynamique du système ?
Sachant que les différences de cinétique de dissolution ne sont pas suffisamment importantes pour craindre un problème de bioéquivalence, quelle est la forme que vous choisiriez ?
Question
Sachant qu'une granulation humide est prévue pour fabriquer un comprimé, ce qui implique un séchage vers 70 °C, quelle stratégie allez-vous mettre en place pour vous assurer que la forme cristalline choisie est bien celle présente en fin de fabrication ?
Question
Les thermogrammes ACD[2] enregistrés cette fois à \(2\ \textrm{°C.min}^{-1}\) sont fournis ci-après. En fonction de la connaissance que vous avez maintenant du type de relation thermodynamique existant entre \(A\) et \(B\), comment interprétez-vous ceux-ci ?
(on précise que les évènements thermiques enregistrés ne comportent aucune transition solide-solide)