Stress intensity factor
When a material subjected to a mechanical stress develops a crack, it can propagate according to several distinct modes: opening (or tensile) mode (method I), sliding mode (method II) or tearing mode (method III) (figure below). The most widely studied mode, because it is most dangerous in crystalline materials, is the opening mode, for which the stresses at crack tip, typically at point \(M\) defined in figure, are expressed as
\(\sigma_{ij} \left( M \right) = \frac{K_I}{\sqrt{2\pi r}} f_{ij} \left( \theta \right)\)
with \(ij = xx, \, yy, \, xy \textrm{ or } yx\)
where \(K_I\) is the stress intensity factor in mode \(I\), \(r\) and \(\theta\) define the position of point \(M\), and \(f_{ij} \left( \theta \right)\) is a trigonometric function.
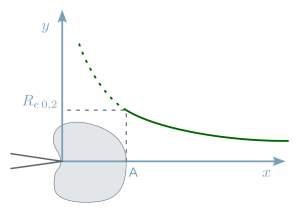
We see that if \(r\) is close to 0, then stress tends toward the infinite, which is of course nonsensical and poses a problem of the validity of the model, developed as part of a linear elastic approach. Furthermore, increase in stresses adjacent to the crack generally leads to the yield strength being exceeded locally, reflected in the appearance of a plastically strained zone whose dimensions are easily estimated by applying the Von Mises plasticity criterion (following figure).
\(\sigma_{xx}=\frac{K_I}{\sqrt{2\pi r}}.\cos\left( \frac{\theta}{2} \right). \left[ 1 - \sin\left( \frac{\theta}{2} \right) . \sin\left( \frac{3\theta}{2} \right) \right]\) | \(\sigma_{xx}=\frac{K_I}{\sqrt{2\pi r}}.\cos\left( \frac{\theta}{2} \right). \left[ 1 - \sin\left( \frac{\theta}{2} \right) . \sin\left( \frac{3\theta}{2} \right) \right]\) |
\(\sigma_{yy}=\frac{K_I}{\sqrt{2\pi r}}.\cos\left( \frac{\theta}{2} \right). \left[ 1 + \sin\left( \frac{\theta}{2} \right) . \sin\left( \frac{3\theta}{2} \right) \right]\) | \(\sigma_{yy}=\frac{K_I}{\sqrt{2\pi r}}.\cos\left( \frac{\theta}{2} \right). \left[ 1 + \sin\left( \frac{\theta}{2} \right) . \sin\left( \frac{3\theta}{2} \right) \right]\) |
\(\sigma_{xy}=\frac{K_I}{\sqrt{2\pi r}}.\cos\left( \frac{\theta}{2} \right). \sin\left( \frac{\theta}{2} \right) . \sin\left( \frac{3\theta}{2} \right)\) | \(\sigma_{xy}=\frac{K_I}{\sqrt{2\pi r}}.\cos\left( \frac{\theta}{2} \right). \sin\left( \frac{\theta}{2} \right) . \sin\left( \frac{3\theta}{2} \right)\) |
\(\sigma_{xz}=\sigma_{yz}=\sigma_{zz}=0\) | \(\sigma_{xz}=\sigma_{yz}=0\) |
\(\sigma_{zz}=\nu \left( \sigma_{xx} + \sigma_{yy}\right) = 0 \quad \textrm{ en contrainte plane}\) | |
plane stress state (surface) | plane strain state (centre) |
|---|
The stress intensity factor \(K_I\) is calculated using the applied stress, the geometry of the part and the size of the crack
\(K_I = \alpha \cdot \sigma _\infty \cdot \sqrt{\pi \cdot a}\)
\(\alpha\) is a geometrical coefficient, for example for a semi-finished plate
\(K_I = 1,12 \cdot \sigma _\infty \cdot \sqrt{\pi \cdot a}\)
where \(a\) is the crack size and, \(\sigma _\infty\) the applied stress
In the case of a plate with a width of \(2W\) :
\(K_I = \cdot \sigma _\infty \cdot \sqrt{\pi \cdot a} \cdot \sqrt {\frac{2W}{\pi \cdot a} \cdot \tan \left( \frac{\pi \cdot a}{2W} \right)}\)
The stress intensity factor increases as size of the crack increases. Even if the nominal stress remains constant, local stresses can increase if the crack grows. When the stress intensity factor reaches a critical value, the stresses are so high that a sudden fracture occurs at the crack tip. This threshold value is called toughness. It is notated as \(K_{IC}\).
Von Mises criterion | Plane strain (middle of the part) |
|---|---|
\(OA = r_y = \frac{1}{2\pi} . \left( \frac{K_I}{R_{0,\,2}} \right) ^2\) | \(r_y = \frac{1}{6\pi} . \left( \frac{K_I}{R_{0,\,2}} \right) ^2\) |