Exercice : Langmuir ou BET ?
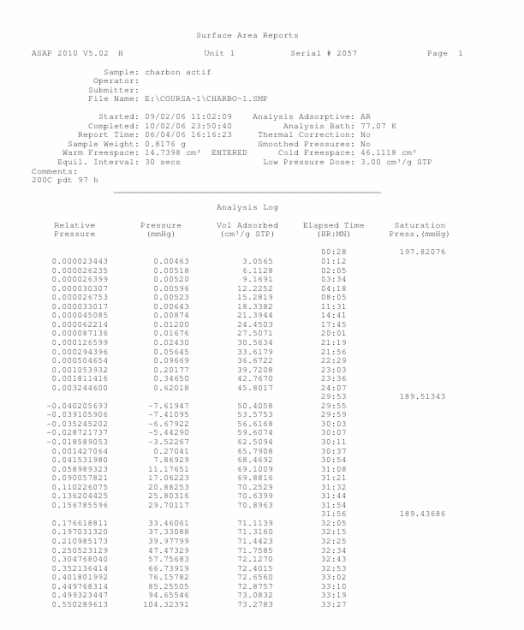
Ci-après est donné le résultat d'une mesure d'isotherme de sorption d'un charbon actif, réalisée avec l'argon comme adsorbat.
Question
Calculer à partir de ces données la surface spécifique de cet échantillon.

Remarque : on notera qu'aux faibles pressions relatives, on a des points de pression négatifs. Ceci est dû au fait que l'on a ici descendu notre vase Deware pour le remplir à nouveau d'azote liquide, ce qui a engendré une perturbation momentanée sur la mesure.
Solution
La loi de Langmuir appliquée à cette isotherme donne \({276}{\, \rm m^2 g^{-1}}\) de surface spécifique tandis que la loi BET appliquée dans un domaine de faibles pressions relatives (entre 0,001 et 0,058) donne une valeur de \({253}{\, \rm m^2 g^{-1}}\).
Solution
Réponse détaillée
Essayons la loi BET : le domaine sur lequel elle est susceptible d'être appliquée est assez restreint, entre 0,04 et 0,13 de pression relative. La constante \(C\) ainsi obtenue est négative : ceci nous indique que la loi BET est mise en défaut ici.

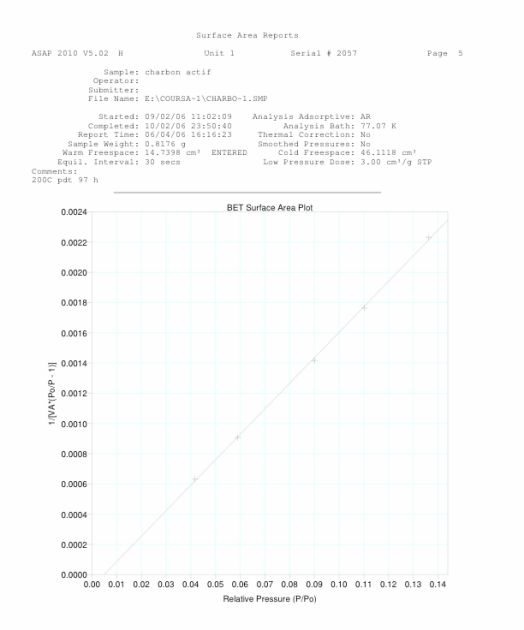
Si l'on sort du domaine classique d'application de la loi BET et si on l'applique à des pressions plus faibles, soit ici entre 0,0010 et 0,0415, en ayant vérifié au préalable l'applicabilité de cette loi, on obtient les résultats suivants :
\(a = {253}{\, \rm m^2 g^{-1}}\)
constante \(C = 987\)
volume de la monocouche : \(V_m = {66,41}{\, \rm cm^3 \, STP / g}\).
coefficient de corrélation de la droit BET ainsi obtenue : 0,9996.
Si on recalcule la pression relative à laquelle on a l'occurrence d'une monocouche, on obtient : \(\left(\frac{P}{P_0}\right)_{\textrm{monocouche}} = \frac{1}{\left(C^{0,5} +1\right)}= 0,03\). Cette valeur de pression relative est bien comprise dans le domaine d'application de la loi.
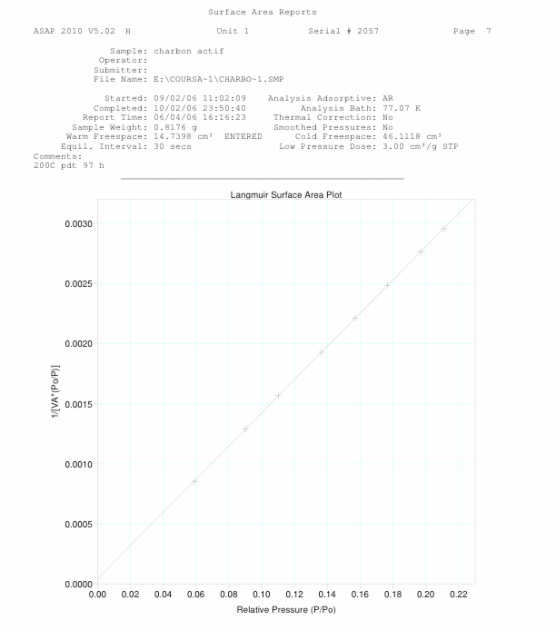
Appliquons maintenant la loi de Langmuir : on trace \(\frac{P/P_0}{V_\textrm{adsorbé}}\) en fonction de \(P/P_0\). La pente de la droite obtenue donne \(1/V_m\) et donc \(V_m\). On a ainsi accès à la surface spécifique :
\(a= \frac{V_m P}{RT} N_{Ar}\varepsilon = {\frac{{72,44..10^{-6}} \cdot 101325}{8,314 \times 273}} \cdot { {6,023.10^{23}} \cdot {0,142.10^{-18}} } = {276,59}{\, \rm m^2 g^{-1}}\)

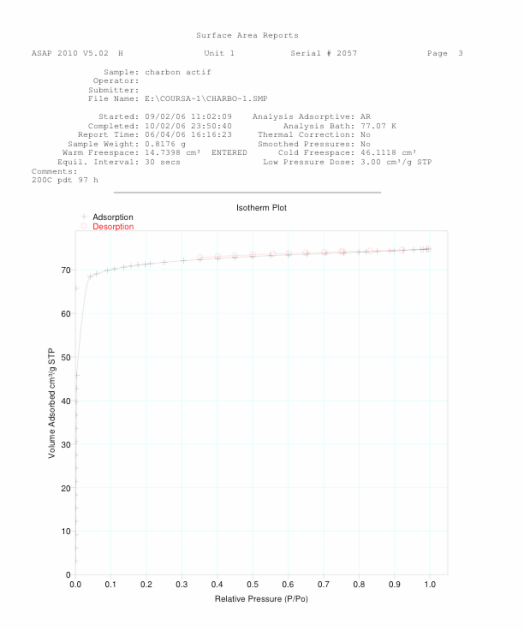
De plus, on peut chercher par régression linéaire l'équation de la droite correspondant au pseudo-palier de l'isotherme d'adsorption (correspondant à la saturation de la mono-couche), soit pour les points de pression relative comprise entre 0,3 et 0,99. Par exemple, si l'on effectue une régression linéaire sur les points de désorption (qui suivent exactement les points d'adsorption), on obtient l'équation :
\(V_\textrm{adsorbé} \, ( { \rm cm^3 g^{-1}}) = 2,870 \left(P/P_0\right) + 72,004\)
L'ordonnée à l'origine de cette droite donne \({72,00}{\, \rm cm^3 g^{-1}}\), ce qui est très proche du volume de la mono-couche obtenue avec la loi de Langmuir, soit \({72,44}{\, \rm cm^3 g^{-1}}\). Donc tout ceci est cohérent et la loi de Langmuir est adéquate dans ce cas.
Conclusion :
La loi de Langmuir semble donc cohérente ici. Sa principale faiblesse est de ne considérer qu'une adsorption mono-couche, ce qui, dans la réalité de l'adsorption physique, est moins justifié que ça ne l'est dans le cas de la chimisorption. L'emploi de la loi BET est, dans ce sens, plus justifié; il faut cependant modifier le domaine de pression sur lequel on l'applique. Et, dans ce cas, est remise l'hypothèse selon laquelle on a qu'un seul type de site en jeu dans cette adsorption. Les deux valeurs ainsi obtenues, celle de Langmuir et celle BET, sont du même ordre de grandeur. Donc, on fait vraisemblablement une erreur dans les deux types de calculs ; ces valeurs sont à considérer de manière relative.