Optimisation numérique

Les méthodes numériques dites recherche de direction sont itératives. Cela a pour conséquences pratiques de :

• définir un « point d'initialisation »

Les calculs vont commencer en ce point dans l'espace de recherche de dimension \(N\). Le choix de ce point d'initialisation ne doit pas être négligé. Parfois un mauvais choix est synonyme d'échec de la mise en œuvre de la méthode.

• répéter les calculs jusqu'à la convergence vers la solution. Il faudra donc à chaque itération vérifier si la solution a été trouvée ; c'est la raison pour laquelle un critère de convergence sera défini et évalué à chaque itération. En pratique, un ou plusieurs critères d'arrêt sont définis et calculés à chaque itération. Ce(s) critère(s) d'arrêt ont pour objectif d'arrêter les calculs car il est fort probable que la solution ne sera jamais trouvée.

Avec ces méthodes, si un minimum est trouvé rien ne garantit que ce soit le minimum global. C'est pour cela qu'il faudra toujours rester critique avec la solution détectée en vérifiant a posteriori que c'est bien un minimum qui a été trouvé. D'autre part, il sera bon d'essayer de trouver l'ensemble des minima pour reconnaître le minimum global. En pratique, le seul moyen pour trouver différents minima avec ces méthodes numériques est de répéter les calculs à partir de points d'initialisation différents.-

Le principe de ces méthodes est de converger itérativement du point d'initialisation vers la solution en déterminant à chaque itération :

• une direction de recherche, notée : \(s[i]\), l'indice \(i\) représente la \(i\)ème itération ; \(s[i]\) est un vecteur de dimension \(N\) ;

• une longueur de déplacement selon cette direction, appelée aussi « pas », notée \(\alpha[i]\), qui est un scalaire.

Le calcul réalisé à chaque itération est donc :

\(x[i+1]=x[i]+\alpha[i]s[i]\)

Les différentes méthodes de type « recherche de direction » vont se distinguer selon leur manière de calculer \(s[i]\) et \(\alpha[i]\).

La direction choisie doit permettre de réduire la valeur courante de la fonction objectif (puisqu'on est dans un problème de minimisation), c'est la raison pour laquelle la direction est appelée direction de descente. On montre géométriquement qu'une direction \(s[i]\) est une direction de descente si elle vérifie l'inégalité suivante au point \(x[i]\) :

\(s[i].\nabla f(x[i])<0\)

On rappelle que \(\nabla f(x[i])\) représente le vecteur gradient calculé en \(x[i]\) et que ce vecteur gradient pointe vers la direction de plus grande augmentation de \(f\) en ce point.

La question est de savoir quelle direction choisir ? Pour cela, on exprime la direction de recherche, \(s[i]\), étant égale à \(-B[i]^{-1}.\nabla f(x[i])\), avec \(B[i]\) est une matrice non singulière et symétrique. L'inégalité précédente devient :

\(s[i].\nabla f(x[i]) = -B[i]^{-1}.\nabla f(x[i]).\nabla f(x[i]) <0\)

Cette égalité n'est vérifiée que dans le cas où \(B[i]\) est une matrice définie positive. Pour définir la direction de recherche, il suffit de choisir une telle matrice.

La méthode la plus connue des méthodes de recherche de descente est celle dite de la plus grande pente où la matrice Identité est choisie à chaque itération, en effet la matrice identité est la matrice définie positive la plus simple. La direction choisie à chaque itération est donc la direction opposée au gradient et correspond à la direction où la fonction f décroit le plus fortement en \(x[i]\) :

\(s[i]=-\nabla f(x[i])\)

La méthode de la plus grande pente est une méthode d'ordre 1 puisqu'elle implique le calcul des dérivées premières de la fonction objectif pour évaluer le vecteur gradient. Elle présente donc la propriété de ne pas nécessiter le calcul de la matrice hessienne, qui est le plus souvent très coûteuse en temps de calcul.

L'algorithme de la méthode de la plus grande pente peut s'écrire :

Il existe de nombreuses méthodes dérivées de la méthode de la plus grande pente. Ces méthodes ont pour but d'augmenter l'efficacité de convergence au détriment de la simplicité. Dans la méthode du gradient conjugué, la différence apportée est dans le calcul de la direction de descente choisie à chaque itération selon la formule :

\(s[i]=-\nabla f(x[i])+\frac{\nabla f(x[i])^T.\nabla f(x[i])}{\nabla f(x[i-1])^T.\nabla f(x[i-1])}.s[i]\)

Le second terme de droite apporte une correction à la direction de la plus grande pente (direction opposée au gradient). Le terme correctif fait intervenir le gradient et la direction de descente de l'itération précédente. C'est la raison pour laquelle on dit qu'il existe un effet mémoire dans cette méthode. La propriété obtenue en calculant des directions de descentes conjuguées entre elles est d'améliorer les performances de convergence ; on démontre même que dans le cas d'une fonction objectif de forme quadratique à n variables alors la convergence à la solution est assurée en n itérations au maximum.

La méthode de Newton est une méthode d'ordre 2 puisqu'elle nécessite l'évaluation de la matrice hessienne, et donc des dérivées secondes de la fonction objectif par rapport aux variables de décision. Comme les méthodes numériques présentées avant, elle est également basée sur des calculs itératifs. Bien que les propriétés théoriques de convergence soient très bonnes (convergence quadratique au voisinage de la solution ; convergence en une itération pour les fonctions objectif de type quadratique), le calcul de la matrice hessienne à chaque itération peut s'avérer très « lourd » et réduit souvent l'intérêt d'utiliser la méthode de Newton.

L'algorithme de la méthode de Newton consiste à déterminer à chaque itération le nouveau point \(x[i+1]\) à partir du précédent en calculant un déplacement \(\Delta x\), déterminé par la résolution du système linéaire suivant :

\(H(x[i]) \Delta x = - \nabla f(x[i])^T\)

puis :

\(x[i+1]=x[i]+\Delta x\)

Dans la formule précédente, \(H(x[i]) \)et \(\nabla f(x[i])\) sont respectivement la matrice hessienne et le gradient de la fonction objectif évalués au point courant.

Le déplacement \(\Delta x\) prend en compte à la fois la direction de recherche et la longueur selon cette direction. Le calcul du déplacement demande donc à chaque itération d'évaluer la matrice hessienne et la résolution d'un système linéaire.

Afin de s'affranchir de certains inconvénients de la méthode de Newton, en particulier des nombreux calculs coûteux en temps, la version de base de la méthode de Newton peut être modifiée par exemple sur les aspects suivants :

1/ Approximations numériques

Le calcul des dérivées premières et/ou secondes pour le vecteur gradient ou la matrice hessienne n'est soit pas possible, soit trop complexe à effectuer. Les dérivées premières et/ou secondes peuvent alors être approximées numériquement par différences finies.

2/ Calcul de la matrice hessienne

Afin de diminuer le temps de calcul, la matrice hessienne n'est calculée qu'une fois toutes les m itérations : on garde la même matrice hessienne pour les itérations : k, k+1, k+2, ... k+m-1. La contrepartie à cette réduction du temps de calcul peut être une dégradation des performances de convergence de la méthode. D'autre part, afin de s'assurer que la matrice hessienne est bien définie positive, elle peut être modifiée afin de la forcer à être définie positive. Par exemple, la méthode de Marquardt emploie la matrice \(H^*(x)\) en lieu et place de la matrice hessienne \(H(x)\).

La matrice \(H^*(x)\) est définie ainsi :

\(H^*(x)=H(x)+\beta I\)

où \(\beta\) est un scalaire positif assez pour s'assurer que \(H^*(x)\) est définie positive.

3/ Introduction d'un facteur de relaxation

La relation itérative de la méthode de quasi-Newton s'écrit maintenant :

\(H(x[i]) \Delta x = - \lambda[i] \nabla f(x[i])^T\)

\(x[i+1]=x[i]+\Delta x\)

En effet, il peut arriver que l'application de la méthode de Newton amène à une augmentation de la fonction objectif. Afin de « freiner » la méthode, on introduit un facteur de relaxation \(\lambda[i]\) qui peut être déterminé empiriquement à chaque itération ou bien choisi constant.

On entend par identification paramétrique la construction d'un modèle représentatif et/ou prédictif et la détermination des paramètres inconnus de ce modèle à partir de données telles que des mesures expérimentales, des relevés de sondage, des données diverses, etc... Ici, la discussion se limitera à la méthode de détermination des paramètres inconnus. Une étape préalable, non abordée ici, est le choix de la structure mathématique du modèle.

La détermination des paramètres inconnus va se faire par la minimisation d'une fonction objectif. C'est donc un problème d'optimisation. Selon la structure du modèle, des techniques d'identification paramétrique plus ou moins simples peuvent être mises en œuvre.

On dispose d'un modèle mathématique (\(g\)), fonction mathématique avec \(n\) paramètres inconnus, stockés dans un vecteur \(x\), (les paramètres sont ici les variables d'optimisation) et avec plusieurs grandeurs d'entrée parfaitement connues et maîtrisées (vecteur \(x\)) et de \(P\) données (ou mesures) dans un vecteur (\(Y\)). Cet ensemble de données a été obtenu à partir de valeurs différentes des grandeurs d'entrée. L'objectif est ici de trouver les paramètres du modèle qui lui permettront de représenter au mieux ces données. Autrement dit, on cherche les valeurs des paramètres pour réduire au maximum l'écart entre les données et les valeurs calculées par le modèle (selon les valeurs des paramètres). On va donc définir une fonction objectif prenant en compte l'ensemble de ces écarts :

\(f(x)=\Sigma_{j=1}^{j=P}(Y_j-g(x,u_j))^2\)

Cette fonction objectif est la somme des écarts au carrés entre les données et les valeurs calculées par le modèle. Si on désigne par \(e\) le vecteur des écarts entre données et modèle alors la fonction objectif peut s'écrire :

\(f(x)=\Sigma_{j=1}^{j=P}(e_j)^2=e(x)^Te(x)\)

\(e(x)\) représente le vecteur des écarts et va dépendre naturellement des valeurs des paramètres \(x\).

La méthode de Gauss-Newton est une application de la méthode de Newton au cas particulier des fonctions objectifs basées sur une somme d'écarts quadratiques. L'algorithme de la méthode de Gauss-Newton consiste donc à déterminer un déplacement \(\Delta x\) à chaque itération pour passer de \(x[i]\) à \(x[i+1]\). La formule est la suivante :

\([E_x^T(x[i]) E_x(x[i])] \Delta x = - E_x^T(x[i]) e(x[i])\)

puis :

\(x[i+1]=x[i]+\Delta x\)

Il y a une grande similitude avec la formule de Newton : un système linéaire doit être résolu à chaque itération pour déterminer l'accroissement. Le système linéaire fait intervenir la matrice jacobienne \(E_x\). La matrice jacobienne est une matrice qui contient les dérivées premières de chaque composante du vecteur \(e(x)\) par chacun des paramètres. C'est donc une matrice de \(P\) lignes et de \(n\) colonnes.

On montre qu'en raison de la formulation bien particulière du problème d'optimisation (fonction objectif quadratique) la condition du second ordre d'existence d'un minimum est toujours vérifiée. Cela implique que si le processus converge, ce sera nécessairement vers un minimum.

Si le modèle dont on recherche les paramètres est linéaire (par rapport aux paramètres) alors le modèle peut s'écrire sous la forme : \(g(x,u)=A x \). \(A\) est une matrice qui contient des constantes et/ou des valeurs de \(u\) ; \(A\) possède autant de lignes que de données (i.e., la dimension du vecteur \(Y\)) et autant de colonnes que de paramètres (dimension du vecteur \(x\)). Le problème d'identification consiste toujours à minimiser la fonction objectif suivante :

\(f(x)=e(x)^Te(x)\)

L'application des conditions du premier ordre d'existence d'un optimum, c'est à dire qu'au minimum de la fonction objectif, la dérivée de celle-ci par rapport à \(x\) est nulle, montre que la solution du problème d'optimisation est :

\(x^*=[A^TA]^{-1}A^TY\)

En pratique, on préférera déterminer \(x^*\) par la résolution du système linéaire suivant :

\(A^TAx^*=A^TY\)

Cette formulation correspond à la méthode des moindres carrés. La méthode des moindres carrés présente l'avantage de ne pas être une méthode itérative.

Comme la méthode des moindres carrés est simple à appliquer, on peut même chercher à l'appliquer à des modèles non-linéaires. Pour cela, il faut être capable de de linéariser au préalable le modèle. Prenons par exemple le modèle :

\(g(x,u)=x_1u^{x_2}\)

Ce modèle est non-linéaire en raison de la puissance en \(x_2\). Il est cependant facilement linéarisable :

\(\log(g(x,u))=\log(x_1u^{x_2)})=\log(x_1)+x_2\log(u)\)

Cette expression est linéaire par rapport aux paramètres, on peut faire un changement de variables (si on veut) :

\(v(x,u)=\log(g(x,u))\log(w_1)+w_2\log(u)\)

La méthode des moindres carrés peut être appliquée. Dans l'exemple, la résolution numériquement permettra d'identifier \(w_1\) et \(w_2\) et il sera nécessaire ensuite d'en déduire les paramètres d'intérêt, c'est à dire \(x_1\) et \(x_2\).

Les méthodes dites d'ordre 0 sont les méthodes d'optimisation qui ne nécessitent pas le calcul de dérivées de la fonction objectif. Une seule méthode est présentée par la suite, connue sous le nom de méthode du simplex de Nelder et Mead (à ne pas confondre avec l'algorithme du Simplexe pour la résolution de problèmes de programmation linéaire). C'est la seule méthode d'optimisation préprogrammée dans MATLAB, hormis celles de la toolbox optimization.

La méthode de Nelder et Mead, appliquée à la recherche du minimum d'une fonction objectif avec \(M\) variables de décision, consiste à calculer les coordonnées de \(M+1\) "sommets" d'une figure géométrique dans l'espace de recherche de dimension \(M\) ; cette figure est appelée simplex. La fonction objectif est évaluée et comparée en chacun des sommets du simplex. Le sommet présentant la valeur maximale de la fonction objectif (c'est donc le sommet avec les moins bonnes performances dans un problème de minimisation) va être remplacé par un nouveau sommet pour ainsi former un nouveau simplex. Le principe est que la valeur de la fonction objectif au nouveau sommet soit plus faible. Le nouveau sommet est le symétrique par rapport au centre de gravité des \(M\) autres sommets du nouveau simplex. La fonction objectif est alors évaluée en ce nouveau sommet et le processus est répété. La recherche du minimum va donc se poursuivre itérativement...

Comme c'est une méthode itérative, un point d'initialisation doit être choisi dans l'espace de recherche. Le simplex initial sera construit autour de ce point. Il faut aussi définir des critères de convergence et d'arrêt. Par exemple, à l'approche du minimum, la taille du simplex peut être réduite afin de localiser la solution avec plus de précision. Un critère de convergence peut être une valeur sur la différence maximale entre les évaluations de la fonction objectif aux différents sommet d'un simplex ; quand la différence est inférieure à cette valeur alors la recherche du minimum est terminée. Un critère d'arrêt peut être le nombre maximal d'itérations.

Ci-dessous, un exemple de construction des premiers simplex dans un problème de maximisation à 2 variables de contrôle ; le simplex est donc un triangle (figure géométrique à 3 sommets dans un plan de dimension 2).

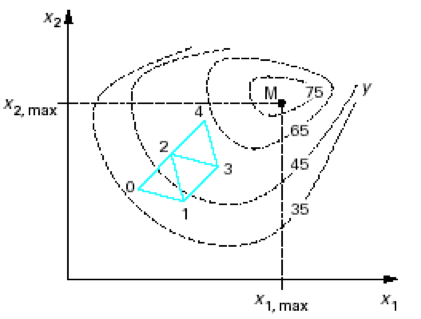
Un problème apparaît si le nouveau sommet choisi (sommet symétrique au plus mauvais sommet) est à son tour le plus mauvais sommet à l'itération suivante. Le processus de calcul va osciller entre ces deux simplex successifs. Pour éviter cela, c'est le sommet symétrique au second plus mauvais sommet qui sera calculé.

L'algorithme peut être amélioré (méthode dite du simplex modifié) en permettant la modification de la taille du simplex à chaque itération afin d'accélérer la convergence vers la solution. Des heuristiques permettent de dilater la taille du simplex s'il est estimé que cela ne va pas dégrader la convergence, ou au contraire réduire la taille du simplex par d'autres heuristiques afin de raffiner la recherche du minimum.

Ce paragraphe donne un focus particulier sur le problème de recherche d'un minimum pour une fonction objectif à une seule variable de contrôle. Les méthodes présentées ici sont spécifiques à ce type de problème et sont appelées méthodes de réduction d'intervalle.

Le principal intérêt de présenter ces méthodes est qu'elles sont employées dans les sous-problèmes d'optimisation de recherche d'un pas optimal selon une direction de descente préalablement déterminée (cf. méthode de la plus grande pente).

Les méthodes de réduction d'intervalle reposent sur l'hypothèse que la fonction objectif est unimodale dans un intervalle de recherche fixé initialement \([a,b]\). Une fonction monovariable est dite unimodale sur un intervalle s'il n'existe qu'un seul minimum dans cet intervalle. L'unimodalité est équivalente à la stricte convexité de la fonction sur cet intervalle dans le cas où celle-ci est continue et deux fois différentiables

La méthode de trichotomie consiste à éliminer un tiers de l'intervalle de recherche à chaque itération. Son principe est le suivant :

1. Choix d'un intervalle initial de recherche \([a,b]\) ;

2. Première itération : \([a,b]\) est partitionné en trois sous-intervalles égaux : les points \(x_1\) et \(x_2\) sont calculés tels que les 3 sous-intervalles \([a,x_1],\)\([x_1,x_2]\) et \([x_2,b]\) soient de même longueur ;

3. Calcul de la valeur de la fonction objectif en \(x_1\)et\(x_2\): \(f(x_1)\) et \(f(x_2)\) ;

4. Élimination d'un des trois sous-intervalle de la recherche :

   si \(f(x_1)>f(x_2)\) alors le minimum, \(x^*\), doit se situer dans  \([x_1,b]\) et donc \([a,x_1]\) peut être retiré de la recherche,

   si \(f(x_1)<f(x_2)\) alors le minimum, \(x^*\), doit se situer dans  \([a,x_2]\) et donc \([x_2,b]\) peut être retiré de la recherche.

5. Seconde itération : le nouvel intervalle de recherche est partitionné en 3 sous-intervalles égaux ...

   etc...

6. Les itérations sont poursuivies jusqu'à ce que l'intervalle de recherche ait une longueur inférieure à une valeur fixée initialement (précision) ;

7. Le minimum, \(x^*\), est considéré au centre de l'intervalle final ; Le minimum est ainsi trouvé à cette précision près.

La méthode de dichotomie se distingue de la précédente méthode par la manière de construire les sous-intervalles. Ici, les trois sous-intervalles ne sont pas égaux. On va maximiser la taille de deux sous-intervalles en les considérant comme presque égaux à la moitié de l'intervalle de recherche en cours :

1. Choix d'un intervalle initial de recherche \([a,b]\) ;

   Première itération : \([a,b]\) est partitionné en trois sous-intervalles non égaux : les points  \(x_1\) et \(x_2\) sont choisis comme \(x_1=x_M-\epsilon\) et \(x_2=x_M+\epsilon\), où \(x_M\) est le centre de l'intervalle de recherche en cours et \(\epsilon\) est une petite valeur correspondant à la précision recherchée ;

2. Calcul de la valeur de la fonction objectif en \(x_1\)et\(x_2\): \(f(x_1)\) et \(f(x_2)\) ;

3. Élimination d'un des trois sous-intervalles de la recherche :

   si \(f(x_1)>f(x_2)\) alors le minimum, \(x^*\), doit se situer dans  \([x_1,b]\) et donc \([a,x_1]\) peut être retiré de la recherche,

   si \(f(x_1)<f(x_2)\) alors le minimum, \(x^*\), doit se situer dans  \([a,x_2]\) et donc \([x_2,b]\) peut être retiré de la recherche.

4. Seconde itération : le nouvel intervalle de recherche est partitionné en 3 sous-intervalles égaux ...

   etc...

5. Les itérations sont poursuivies jusqu'à ce que l'intervalle de recherche ait une longueur inférieure à une valeur fixée initialement (précision) ;

6. Le minimum, \(x^*\), est considéré au centre de l'intervalle final ; Le minimum est ainsi trouvé à cette précision près.

La méthode de la recherche dorée permet de réduire le nombre de calculs en comparaison avec les deux précédentes méthodes. Ses deux principes sont qu'à chaque itération, le rapport de la longueur de la région éliminée sur la longueur de la région précédente doit être constant et qu'une seule évaluation de fonction ait lieu :

1. Choix d'un intervalle initial de recherche \([a,b]\) ;

   Première itération : \([a,b]\) est partitionné en trois sous-intervalles non égaux : les points  \(x_1\) et \(x_2\) sont choisis comme \(x_1=b-0.618 L_0\) et \(x_2=a+0.618 L_0\), où \(L_0\) est la longueur de l'intervalle initial \([a,b]\) ;

2. Calcul de la valeur de la fonction objectif en \(x_1\)et\(x_2\): \(f(x_1)\) et \(f(x_2)\) ;

3. Élimination d'un des trois sous-intervalle de la recherche :

   cas a : si \(f(x_1)>f(x_2)\) alors le minimum, \(x^*\), doit se situer dans  \([x_1,b]\) et donc \([a,x_1]\) peut être retiré de la recherche,

   cas b : si \(f(x_1)<f(x_2)\) alors le minimum, \(x^*\), doit se situer dans  \([a,x_2]\) et donc \([x_2,b]\) peut être retiré de la recherche.

4. Seconde itération : le nouvel intervalle de recherche est partitionné en 3 sous-intervalles égaux : un seul nouveau point est déterminé ; en effet :

   cas a : \(x_1 -> a ; x_2 -> x_1\) et une nouvelle valeur de \(x_2 :\) \(x_2=a+0.618 L_i\)

   cas b : \(x_2 -> b ; x_1 -> x_2\) et une nouvelle valeur de \(x_1 :\) \(x_1=b-0.618 L_i\)

   avec \(L_i\) la longueur de l'intervalle de recherche à l'itération i ;

   etc...

5. Les itérations sont poursuivies jusqu'à ce que l'intervalle de recherche ait une longueur inférieure à une valeur fixée initialement (précision) ;

6. Le minimum, \(x^*\), est considéré au centre de l'intervalle final ; Le minimum est ainsi trouvé à cette précision près.

Pour juger de la performance d'une méthode, sa capacité à réduire l'intervalle de recherche à chaque itération est évaluée. Si on appelle, \(\rho_k\), le facteur de réduction à l'itération k, c'est à dire le ratio de la longueur de l'intervalle de recherche à l'itération k, \(L_k\), sur l'intervalle de recherche initial \(L_0\) alors il est aisé de comparer les méthode.

Pour la méthode de trichotomie, il est aisé de montrer que : \(\rho_k=(2/3)^k\)

Pour la méthode de dichotomie, c'est un peu plus compliqué, mais il est possible de montrer que \(\rho_k\) converge vers une valeur finie égale à \(\epsilon/L_0\)

Pour la méthode de recherche dorée : \(\rho_k=(0.618)^k\)

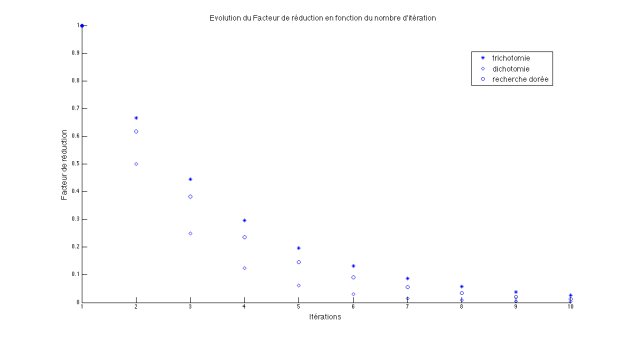
Sur la figure ci-dessous est représentée l'évolution du facteur de réduction des trois méthodes lors des 10 premières itérations sur un exemple donnée. On constate que sur les premières itérations, la méthode de dichotomie permet de réduire le plus le facteur de réduction, mais très vite les différentes méthodes sont très proches. Cependant, il faut en prendre en compte que la méthode de recherche dorée n'évalue la fonction objectif qu'une fois par itération alors que les deux autres méthodes demandent deux évaluations de fonction par itération.