Résolution analytique
Un exemple introductif
Nous allons poser un premier problème d'optimisation avec contraintes grâce à un exemple simple de géométrie.
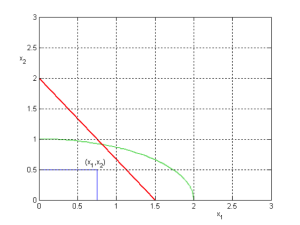
On cherche à définir un rectangle de surface maximale dans le quadrant positif du plan cartésien. Le rectangle doit se situer sous une ellipse donnée (équation fournie) et les coordonnées de l'angle supérieur droit du rectangle doivent se situer sur une droite donnée (équation fournie). Une représentation graphique du problème est donnée sur la figure ci-dessous
On cherche à avoir le rectangle (en bleu) le plus grand possible. Si on désigne par \(x_1\) et \(x_2\) les coordonnées de l'angle supérieur droit du rectangle, les contraintes imposent que ce point soit sous l'ellipse (en vert) et se situe sur la droite (en rouge)
L'analyse du problème permet d'identifier que les variables sont au nombre de deux (\(x_1\) et \(x_2\) ). La fonction objectif correspond à l'aire du rectangle. Le problème d'optimisation s'écrit : \(Max~~~ x_1x_2\)
Par convention et aussi en raison des choix faits par la plupart des outils logiciels, on va exprimer tout problème d'optimisation sous forme d'un problème de minimisation. Si on cherche à maximiser une fonction, il est alors nécessaire de transformer la fonction objectif. Cette transformation n'est pas unique et suivant les cas, certaines transformations peuvent s'avérer plus pertinentes que d'autres, par exemple pour des raisons de facilité d'implantation numérique. Dans l'exemple traité, on peut par exemple proposer de minimiser \(1/x_1x_2\)ou bien de minimiser \(-x_1x_2\). En effet, on peut démontrer que : \(Max~~~ f~~~=~~~Min~~~ -f\)
Sans précision supplémentaire et par défaut, il sera toujours choisi cette dernière transformation. Donc le problème de minimisation s'écrit dans notre exemple : \(Min~~~ -x_1x_2\)
Une fois la fonction objectif et les variables de contrôle définies, il faut étudier le domaine d'existence de ces dernières. Ici, il n'y a pas de bornes supérieures sur les variables, par contre des bornes inférieures sont fournies puisque le rectangle doit s'inscrire dans le quadrant positif : \(x_1≥0\) et \(x_2≥0\)
L'exemple contient une contrainte dite contrainte égalité : les coordonnées de l'angle supérieur droit se situent sur une droite donnée. L'expression mathématique de la contrainte égalité, notée \(h_1\) , correspond à l'expression de la droite suivante : \(h_1(x_1,x_2)=20*x_1+15*x_2-30=0\).
L'exemple contient une contrainte dite contrainte inégalité : le rectangle, et donc les coordonnées de l'angle supérieur droit, se situe sous une ellipse donnée. L'expression mathématique de la contrainte inégalité, notée \(g_1\), correspond à l'équation de l'ellipse suivante : \(g_1(x_1,x_2)=(x_1/2)^2+x_2^2-1≤0\).
Définition :
Le problème à résoudre s'écrit donc finalement :
\(Min~~~ -x_1x_2\)
\(h_1(x_1,x_2)=20*x_1+15*x_2-30=0\)
\(g_1(x_1,x_2)=(x_1/2)^2+x_2^2-1≤0\)
\(0≤x_1\) et \(0≤x_2\)
Fondamental :
La formulation générale d'un problème d'optimisation non-linéaire sous contraintes (abréviation NLP pour Nonlinear Programming Problem) est :
\(Min~~~ f(x_1,x_2,...,x_n)\)
\(h_k(x_1,x_2)=0~~~~~~ k=1,2,... K\)
\(g_j(x_1,x_2)≤0~~~~~~ j=1,2,... J\)
\(x_i^l≤x_i≤x_i^u~~~~~~ i=1,2,... N\)
f est la fonction objectif dépendant de n variables de contrôle (\(x_1\), \(x_2\),...\(x_n\) ). K contraintes égalité (\(h_k\)) et J contraintes inégalité (\(g_j\)) viennent compléter le problème. Les N variables ont éventuellement des domaines de définition dans un intervalle compris entre une bonne inférieure (\(x^l\)) et une borne supérieure (\(x^u\)). Cette formulation peut également s'écrire sous notation vectorielle :
\(Min~~~ f(X)\)
\([h(X)]_K=0\)
\([g(X)]_J≤0\)
\(X^l≤X≤X^u\)
Conditions d'existence d'un extremum
On appelle conditions de Kunh-Tucker, les conditions du premier ordre appliquée à la fonction lagrangienne associée au problème d'optimisation NLP. La fonction Lagrangienne (\(L\) ) est une fonction mathématique qui peut être définie une fois le problème d'optimisation sous contraintes posé ; elle est égale à la somme de la fonction objectif (\(f\) ) et d'une combinaison linéaire des contraintes. Les coefficients de cette combinaison linéaire sont appelés multiplicateurs de Lagrange (\(\lambda\) et \(\beta\)) :
\(L(x_1,...,x_n,\lambda_1,...,\lambda_K,\beta_1,...,\beta_J)=f(x_1,...,x_n)+\lambda_1*h_1+...+\lambda_K*h_K+\beta_1*g_1+...+\beta_j*g_J\)
On démontre que la solution du problème NLP correspond à la solution de ce problème d'optimisation :
\(Min~~~ L(x_1,x_2,...,x_n,\lambda_1,...,\lambda_K,\beta_1,...,\beta_J)\)
On passe donc d'un problème d'optimisation avec contraintes à un problème sans contrainte mais on a augmenté le nombre d'inconnues (\(x_i,\lambda_k,\beta_j\)). On peut alors résoudre analytiquement ce problème d'optimisation sans contrainte (c'est possible dans les cas simples), en exprimant les conditions du premier ordre à la fonction lagrangienne, c'est à dire :
\(\frac{dL}{dx_i}=0~~~~i=1,2,...,N\)
\(\frac{dL}{d\lambda_k}=h_k=0~~~~ k=1,2,... K\)
\(\frac{dL}{d\beta_j}=\beta_j*g_j=0~~~~ j=1,2,... J\)
Solution analytique d'un problème d'optimisation avec seulement des contraintes égalité
Le nombre de contraintes égalité doit être inférieur à la dimension du problème d'optimisation : \(K<N\).
Dans le cas où seules des contraintes égalité existent, la fonction lagrangienne associée au problème d'optimisation s'écrit :
\(L(x_1,...,x_n,\lambda_1,...,\lambda_K)=f(x_1,...,x_n)+\lambda_1*h_1+...+\lambda_K*h_K\)
A la solution, les conditions du premier ordre sont vérifiées :
\(\frac{dL}{dx_i}=0~~~~i=1,2,...,N\)
\(\frac{dL}{d\lambda_k}=h_k=0~~~~ k=1,2,... K\)
La résolution analytique consiste donc à trouver la solution d'un système de N+K équations algébriques à N+K inconnues.
Remarque :
Il existe une condition du second ordre (non détaillée ici) qui impose qu'à la solution la matrice hessienne de la fonction lagrangienne soit définie positive. En pratique, cette condition du second ordre est très peu utilisée car très lourde à mettre en œuvre.
Remarque : Signification du multiplicateur de Lagrange
Le multiplicateur de Lagrange a une signification que nous allons illustrer sur un exemple. Soit la fonction de Lagrange suivante :
\(L(x_1,x_2,\lambda_1)=f(x_1,x_2)+\lambda_1*h_1\)
On montre :
\(dL=df+\lambda_1*dh_1=\frac{dL}{dx_1}dx_1+\frac{dL}{dx_2}dx_2+\frac{dL}{d\lambda_1}d\lambda_1\)
A la solution (\(dL=0\)), soit:
\(\lambda_1=-\frac{df}{dh_1}=-\frac{\Delta f}{\Delta h_1}\)
Le multiplicateur de Lagrange représente le rapport de la variation de la fonction objectif sur la variation de la contrainte \(h_1\) à la solution.
Remarque : Solution par substitution
Dans certains problèmes simples NLP, il est possible de trouver la solution par substitution des contraintes dans la fonction objectif. Illustrons ceci par l'exemple suivant :
\(Min~~~ f(x_1,x_2)\)
\(h_1(x_1,x_2)=0\)
Si la contrainte \(h_1\) peut se mettre sous la forme : \(x_1=hh_1(x_2)\) alors il suffit alors d'injecter cette expression de \(x_1\) dans la fonction objectif pour se ramener à un problème d'optimisation sans contrainte à une seule variable. Cependant, attention dans certains cas, la substitution peut amener à une mauvaise solution ! Par exemple, soit le problème suivant :
\(Min~~~ x_1^2+x_2^2\)
\((x_1-1)^2-x_2^2=0\)
On peut facilement injecter une expression de \(x_2\) issue de la contrainte dans la fonction objectif et se ramener à un problème d'optimisation à une seule variable sans contrainte. Cependant dans cet exemple, la contrainte imposait implicitement que \((x_1>1\), ce qui ne sera plus vrai si le problème d'optimisation initial est transformé.
Solution analytique d'un problème d'optimisation avec seulement des contraintes inégalité
Considérons le cas d'un problème NLP avec seulement des contraintes inégalité. Le nombre de contraintes inégalité (\(J\)) peut être supérieur à la dimension du problème d'optimisation (\(N\)), mais seules (\(N-1\)) contraintes peuvent être "saturées" en même temps. Une contrainte inégalité est dite saturée quand la solution se situe à sa limite, c'est quand l'égalité est vérifiée.
Afin de résoudre analytiquement ce type de problème, les contraintes inégalité sont transformées en contrainte égalité. Cette transformation est basée sur l'ajout d'une variable supplémentaire par contrainte inégalité ; cette nouvelle variable est appelée variable d'écart. Ainsi à chaque contrainte inégalité \(j\), une variable \(y_j\) est définie puisque si \(g_j≤0\) alors il existe une valeur de \(y_j\) telle que \(g_j+y_j^2=0\)
La fonction de Lagrange associée au problème NLP devient :
\(L(x_1,...,x_n,\beta_1,...,\beta_J,y_1,...,y_J)=f(x_1,...,x_n)+\beta_1*(g_1+y_1^2)+...+\beta_J*(g_J+y_J^2)\)
Il y a \(N+2J\) inconnues (\(x_i,y_j,\beta_j\)).
Les conditions du premier ordre, c'est à dire l'annulation des dérivés de la fonction Lagrangienne par rapport aux \(N+2J\) inconnues, conduisent à la résolution d'un système de \(N+2J\) équations algébriques.
Les dérivées de la fonction Lagrangienne par rapport aux \(y_j\) s'écrivent :
\(\frac{dL}{dy_j}=2*\beta_j*y_j=0~~~~ j=1,2,... J\)
Cette égalité est vraie :
si \(\beta_j=0\), ce qui implique que \(y_j≠0\) et donc \(g_j<0\) ;
si \(y_j=0\) , ce qui implique que \(g_j=0\) et donc \(\beta_j≠0\), la contrainte inégalité est alors saturée.
Il existe une condition du second ordre (non détaillée) qui impose qu'à la solution la matrice hessienne de la fonction lagrangienne soit définie positive et que \(\beta_j≥0\).
Bilan : conditions de Karush-Kunh-Tucker (KKT)
L'existence d'une solution pour un problème NLP peut se résumer par le théorème de Karush-Kunh-Tucker. Les conditions nécessaires (mais pas suffisantes) du premier ordre de Karush-Kunh-Tucker établissent que si \(x^*\) est un minimum local d'un problème NLP alors il existe un vecteur
\([\lambda^*,\beta^*]^T\) de multiplicateurs de Lagrange tel que les conditions suivantes soient satisfaites en \((x^*,\lambda^*,\beta^*)\) :
\(\frac{dL(x^*,\lambda^*,\beta^*)}{dx_i}=0~~~~i=1,2,...,N\)
\(h_k(x^*)=0~~~~ k=1,2,... K\)
\(g_j(x^*)≤0~~~~ j=1,2,... J\)
\(\beta_j^*≥0~~~~ j=1,2,... J\)
\(\beta_j^*g_j(x^*)≤0~~~~ j=1,2,... J\)
Les conditions suffisantes du second ordre de Karush-Kunh-Tucker établissent que si \((x^*,\lambda^*,\beta^*)\) vérifient les conditions du premier ordre et si la matrice Hessienne de la fonction de Lagrange est définie positive alors \(x^*\) est un minimum local.